Some Context: This post is a shortened version of a paper that won the best-paper award at FUN 2020. The paper is ostensibly about trains but the real-world applicability may be somewhat… limited. The actual purpose of the paper is educational: we get to see some of the funnest techniques in probabilistic combinatorics being used to solve a cute problem involving trains.
Part 1: A Consequential Train Ride
A few years ago, while traveling on a train, and on only a few hours of sleep, I was staring out the window. The train crossed a bridge over a road, and the ground was momentarily replaced by a steep drop. Startled, my sleep-deprived mind briefly wondered whether there was still a track underneath us. “Of course there is,” I thought to myself. “Without a track, the train car would have fallen into the gap.”
“Ah, no so fast!” responded the latent mathematician inside me. “If the train car had more than two sets of wheels, then perhaps it could cross the bridgeless gap without falling in.” It was true.
Consider, for example, a train with four sets of wheels: one set in the rear, one set in the front, and one set in each of the first and third quartiles.

As long as the gap in the track is less than the distance between any pair of wheels, then at least three sets of wheels will touch track at all times. Assuming that the center of mass of the train is in the middle half of the train, then the the train does not fall into the gap.
“In fact,” continued the latent mathematician, “what if we have  sets of wheels? Maybe we can build a mono-rail using an asymptotically small amount of track.”
sets of wheels? Maybe we can build a mono-rail using an asymptotically small amount of track.”
“That’s a stupid idea,” responded I. “Gaps in train track are not something to optimize.”
But I was sleep deprived, so I did it anyway.
The Basic Observation: More Wheels Means Less Track.
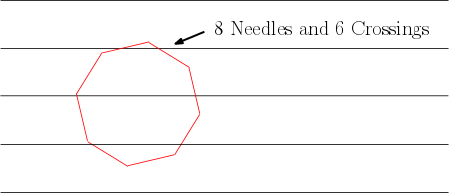
Consider a train car with  sets of wheels. Half the sets are evenly dispersed across the first quarter of the train car, and half the sets are evenly dispersed across the final quarter. The train can safely drive down the track as long as at least one set of wheels from each side of the train car is touching track at all times. The train car looks something like this:
sets of wheels. Half the sets are evenly dispersed across the first quarter of the train car, and half the sets are evenly dispersed across the final quarter. The train can safely drive down the track as long as at least one set of wheels from each side of the train car is touching track at all times. The train car looks something like this:
Want to build a monorail, but you’re short on track? No problem! You can get away with filling in only an  fraction of the track:
fraction of the track:

Every quarter of a train length, we place a piece of track whose length is a 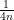 fraction of the length of the train car. We get asymptotic cost savings!
fraction of the length of the train car. We get asymptotic cost savings!
To see that this is the best we can do, suppose that the fraction of track that is filled in is less than 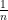 , and for symmetry sake suppose the track is circular (i.e., the end of the track loops back to the start). If we place the train at a random position in the circular track, then each wheel has a less than
, and for symmetry sake suppose the track is circular (i.e., the end of the track loops back to the start). If we place the train at a random position in the circular track, then each wheel has a less than 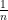 chance of touching track. By a union bound, it follows that the probability of any wheel in the rear quarter of the train touching the track is less than
chance of touching track. By a union bound, it follows that the probability of any wheel in the rear quarter of the train touching the track is less than  . Thus no matter how the track is placed, if the total fraction of track that is filled in is less than
. Thus no matter how the track is placed, if the total fraction of track that is filled in is less than 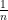 , then there is some position at which the train falls through.
, then there is some position at which the train falls through.
Part 2: Trains with Non-Uniform Wheel Placements
Consider a train car that has  wheels in its rear quarter and
wheels in its rear quarter and  wheels in its front quarter, but suppose that the wheels aren’t evenly spaced. For example, maybe the rear of the car looks something like this:
wheels in its front quarter, but suppose that the wheels aren’t evenly spaced. For example, maybe the rear of the car looks something like this:
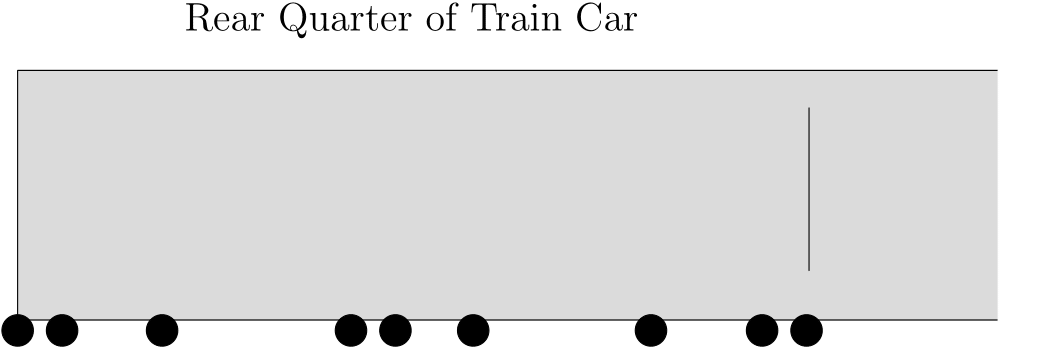
Can we still fill in an asymptotically small fraction of the track in a way that will allow the train car to drive down the track? In other words, can we place down a small amount of track in a way so that, as the train drives down it there is always at least one wheel from each of the front and rear quarters of the train touching track? It turns out that, via a simple application of the probabilistic method with alterations, we can.
To formalize the situation, let’s focus just on the first quarter of the train. (In particular, up to a constant factor in the amount of train track that we install, we can consider the two quarters of the train separately.) Suppose this portion of the train is  feet long, and assume that each of the
feet long, and assume that each of the  sets of wheels resides at a distinct integer offset from the rear of the train. Our goal is to build a train track that is
sets of wheels resides at a distinct integer offset from the rear of the train. Our goal is to build a train track that is 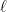 feet long. We build the train track out of pillars that are each
feet long. We build the train track out of pillars that are each  foot long and are each placed at integer positions on the track. We are required to put down the pillars in a way so that, as the train drives down the track, at least one wheel from the rear quarter is always touching the track (i.e., touching some pillar). We want to use as little track as possible, with the best we could hope for being a total of
foot long and are each placed at integer positions on the track. We are required to put down the pillars in a way so that, as the train drives down the track, at least one wheel from the rear quarter is always touching the track (i.e., touching some pillar). We want to use as little track as possible, with the best we could hope for being a total of 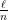 pillars.
pillars.
As a reminder, there are three variables: the number of wheels  (in the quarter of the train car that we’re considering), the length
(in the quarter of the train car that we’re considering), the length  of one quarter of the train car, and the length
of one quarter of the train car, and the length 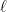 of the train track. In general, we have
of the train track. In general, we have  . Note that, although
. Note that, although  and
and  could reasonably be close to one another (e.g.,
could reasonably be close to one another (e.g.,  ), we also want to be able to handle cases where
), we also want to be able to handle cases where  . This allows for the train car to be configured in truly strange ways — for example, the positions of the wheels could even form a geometric series:
. This allows for the train car to be configured in truly strange ways — for example, the positions of the wheels could even form a geometric series:

A Randomized Algorithm for Building Track.
Our algorithm for deciding where to put the pillars is a simple example of the probabilistic method with alterations. In particular, we begin by randomly constructing a track that uses only a small number of pillars, and then we show that this track can be slightly altered in order to support (the rear quarter of) the train car at every point. The result will be a train track of length 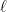 using only
using only  pillars (and as we shall see later, this is optimal).
pillars (and as we shall see later, this is optimal).
We begin by installing each pillar randomly with probability 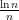 . Even though this strategy has nothing to do with the structure of where the wheels are on the train, it already does remarkably well. In particular, if we place the train at some given position on the track, then there are
. Even though this strategy has nothing to do with the structure of where the wheels are on the train, it already does remarkably well. In particular, if we place the train at some given position on the track, then there are  different pillar positions that could potentially hold up the rear quarter. Each of these pillars positions has a
different pillar positions that could potentially hold up the rear quarter. Each of these pillars positions has a 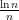 probability of having a pillar installed. It follows that, for a given position on the track, the rear quarter of the train has a
probability of having a pillar installed. It follows that, for a given position on the track, the rear quarter of the train has a
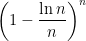
probability of falling through the track. Taking advantage of the identity  , which holds for any
, which holds for any 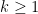 , we see that the wheels fall through the track with probability at most,
, we see that the wheels fall through the track with probability at most,
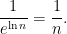
In other words, out of all the places we can place the train on the track, only a 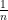 -fraction of them will be problematic (in expectation). To fix this, we can just install one additional pillar to remedy each of these problematic positions. The result is a train track that fully supports the rear quarter of our train, and that uses only
-fraction of them will be problematic (in expectation). To fix this, we can just install one additional pillar to remedy each of these problematic positions. The result is a train track that fully supports the rear quarter of our train, and that uses only 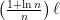 total feet of track, in expectation.
total feet of track, in expectation.
The construction is kind of fun to visualize. We start with some random pillars, and then we add additional pillars as needed so that the train never falls through the track:

Of course, our bound of 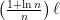 isn’t quite as good as we did when the wheels were evenly spaced out (we are a roughly
isn’t quite as good as we did when the wheels were evenly spaced out (we are a roughly  factor worse). But it’s still pretty amazing! No matter how the wheels are distributed across each quarter of the train car, we can get away with installing only a
factor worse). But it’s still pretty amazing! No matter how the wheels are distributed across each quarter of the train car, we can get away with installing only a 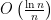 fraction of the track!
fraction of the track!
Part 3: A Matching Lower Bound
In the rest of this post, we’re going to prove that the construction above is optimal. (This is where the math gets really cool.) That is, we’ll show that there exists a train car configuration for which 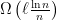 pillars are necessary. We are going to again use the probabilistic method, but this time in a more sophisticated way.
pillars are necessary. We are going to again use the probabilistic method, but this time in a more sophisticated way.
We continue to focus only on the rear quarter of the train car, which is  feet long. We set
feet long. We set  , and we will construct the rear quarter of the train car by placing
, and we will construct the rear quarter of the train car by placing  wheels at integer positions in the set
wheels at integer positions in the set  . We will then consider a track of length
. We will then consider a track of length  , and show that
, and show that  pillars are necessary in order to support the rear quarter of the train car at all positions on the track. Recall that each pillar is one foot wide and is placed at an integer offset on the track.
pillars are necessary in order to support the rear quarter of the train car at all positions on the track. Recall that each pillar is one foot wide and is placed at an integer offset on the track.
Let 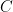 be the set of wheel-positions in the rear quarter of the train car. We choose
be the set of wheel-positions in the rear quarter of the train car. We choose 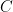 by placing a wheel at each position in
by placing a wheel at each position in  independently with probability
independently with probability 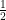 . This means that
. This means that 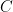 has
has  wheels in expectation, but may not actually have exactly
wheels in expectation, but may not actually have exactly  wheels. The important thing to note is that, with at least
wheels. The important thing to note is that, with at least  probability,
probability, 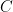 has
has  or more wheels.
or more wheels.
Now consider a track layout given by a subset  of
of  , and satisfying
, and satisfying  . Whereas
. Whereas 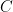 is a random variable,
is a random variable,  is a fixed set.
is a fixed set.
Define  to be the event that, for every possible position of the rear quarter of the train on the track, at least one wheel from the rear quarter of the train is supported by track. From the perspective of the train car,
to be the event that, for every possible position of the rear quarter of the train on the track, at least one wheel from the rear quarter of the train is supported by track. From the perspective of the train car,  is a good event. Formally,
is a good event. Formally,  occurs if for every offset
occurs if for every offset 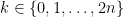 , we have
, we have 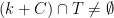 .
.
The key to proving the desired lower bound is to show that the probability of  occurring is very small, namely that
occurring is very small, namely that ![{\Pr[X_{C, T}] < \frac{1}{2 \binom{4n}{(\ln n) / 4}}}](https://s0.wp.com/latex.php?latex=%7B%5CPr%5BX_%7BC%2C+T%7D%5D+%3C+%5Cfrac%7B1%7D%7B2+%5Cbinom%7B4n%7D%7B%28%5Cln+n%29+%2F+4%7D%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . Because
. Because  is a
is a 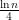 -element subset of
-element subset of  , there are at most
, there are at most  possibilities for
possibilities for  . Taking a union bound over all of these possibilities implies that
. Taking a union bound over all of these possibilities implies that
![\displaystyle \Pr[X_{C, T} \text{ for any }T] < \frac{1}{2}.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5CPr%5BX_%7BC%2C+T%7D+%5Ctext%7B+for+any+%7DT%5D+%3C+%5Cfrac%7B1%7D%7B2%7D.&bg=ffffff&fg=000000&s=0&c=20201002)
On the other hand, we know that the number of wheels 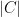 is less than
is less than  with probability at most
with probability at most 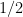 . By a union bound, the probability that either
. By a union bound, the probability that either 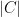 has fewer than
has fewer than  wheels or that
wheels or that  holds for some
holds for some  is less than
is less than  . Hence there must exist a car
. Hence there must exist a car 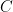 with
with  or more sets of wheels, and such that no track
or more sets of wheels, and such that no track  of size smaller than
of size smaller than 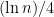 satisfies
satisfies  . In fact, with slightly more careful bookkeeping, one can show that an even stronger property is true: almost all choices of how to place
. In fact, with slightly more careful bookkeeping, one can show that an even stronger property is true: almost all choices of how to place  wheels in
wheels in 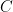 require a track of size larger than
require a track of size larger than 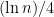 to support the car.
to support the car.
To complete the lower bound, the challenge becomes to show that ![{\Pr[X_{C, T}]}](https://s0.wp.com/latex.php?latex=%7B%5CPr%5BX_%7BC%2C+T%7D%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) is very small. That is, for a given choice of track
is very small. That is, for a given choice of track  containing
containing  pillars, the probability that
pillars, the probability that  supports the rear-quarter of the train car
supports the rear-quarter of the train car 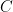 is small.
is small.
Rather than examine the event  directly, we instead examine a related quantity. Define
directly, we instead examine a related quantity. Define 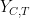 to be the number of positions
to be the number of positions 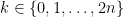 for which
for which  (i.e., the number of positions in which the rear quarter of the car, given by
(i.e., the number of positions in which the rear quarter of the car, given by 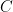 , falls through the track
, falls through the track  ).
).
The relationship between  and
and 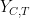 is that
is that  occurs if and only if
occurs if and only if  . Our approach to completing the analysis will be to first show that
. Our approach to completing the analysis will be to first show that ![{\mathop{\mathbb E}[Y_{C, T}]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cmathbb+E%7D%5BY_%7BC%2C+T%7D%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) is relatively large, and then to show that the probability of
is relatively large, and then to show that the probability of 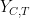 deviating substantially from its expected value is small. This, in turn, implies that
deviating substantially from its expected value is small. This, in turn, implies that ![{\Pr[Y_{C, T} = 0]}](https://s0.wp.com/latex.php?latex=%7B%5CPr%5BY_%7BC%2C+T%7D+%3D+0%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) is small, completing the analysis. In other words, the problem of proving that there exists a train-car configuration requiring a large amount of track is reduced to the problem of proving a concentration inequality on the random variable
is small, completing the analysis. In other words, the problem of proving that there exists a train-car configuration requiring a large amount of track is reduced to the problem of proving a concentration inequality on the random variable 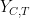 .
.
For each position 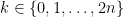 , the set
, the set  consists of
consists of 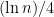 elements. Since each of these elements is contained in
elements. Since each of these elements is contained in 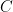 with probability
with probability 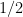 , the probability that
, the probability that 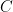 avoids all of the elements in
avoids all of the elements in  is given by,
is given by,
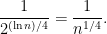
Summing over the values of  , it follows that the expected number of positions
, it follows that the expected number of positions  in which
in which 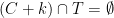 is
is
![\displaystyle \mathop{\mathbb E}[Y_{C, T}] = 2n \cdot \frac{1}{n^{1/4}} > n^{3/4}.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cmathop%7B%5Cmathbb+E%7D%5BY_%7BC%2C+T%7D%5D+%3D+2n+%5Ccdot+%5Cfrac%7B1%7D%7Bn%5E%7B1%2F4%7D%7D+%3E+n%5E%7B3%2F4%7D.&bg=ffffff&fg=000000&s=0&c=20201002)
The final step of the analysis is to prove a concentration inequality on 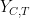 . Standard Chernoff bounds do not apply here because
. Standard Chernoff bounds do not apply here because 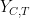 is not a sum of independent indicator random variables. Instead, we employ a more powerful tool, namely McDiarmid’s Inequality:
is not a sum of independent indicator random variables. Instead, we employ a more powerful tool, namely McDiarmid’s Inequality:
McDiarmid’s Inequality (1989): Let  be independent random variables over an arbitrary probability space. Let
be independent random variables over an arbitrary probability space. Let  be a function mapping
be a function mapping  to
to 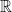 , and suppose
, and suppose  satisfies,
satisfies,

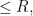
for all 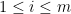 . That is, if
. That is, if 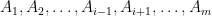 are fixed, then the value of
are fixed, then the value of 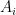 can affect the value of
can affect the value of 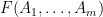 by at most
by at most 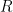 ; this is known as the Lipschitz Condition. Then for all
; this is known as the Lipschitz Condition. Then for all 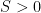 ,
,
![\displaystyle \Pr[|F(A_1, \ldots, A_m) - \mathop{\mathbb E}[F(A_1, \ldots, A_m)]| \ge R \cdot S] \le 2e^{-2S^2 / m}.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5CPr%5B%7CF%28A_1%2C+%5Cldots%2C+A_m%29+-+%5Cmathop%7B%5Cmathbb+E%7D%5BF%28A_1%2C+%5Cldots%2C+A_m%29%5D%7C+%5Cge+R+%5Ccdot+S%5D+%5Cle+2e%5E%7B-2S%5E2+%2F+m%7D.&bg=ffffff&fg=000000&s=0&c=20201002)
To apply McDiarmid’s Inequality to our situation, recall that 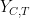 is defined to be the number of positions in the track
is defined to be the number of positions in the track  that the rear quarter of the car, given by
that the rear quarter of the car, given by 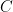 , falls through. Whereas the track
, falls through. Whereas the track  is fixed, each of the
is fixed, each of the  possible wheels in
possible wheels in 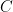 is picked with probability
is picked with probability 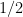 . Define the indicator random variables
. Define the indicator random variables  so that
so that 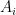 indicates whether
indicates whether 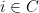 . As required by McDiarmid’s Inequality, the
. As required by McDiarmid’s Inequality, the 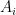 ‘s are independent of one-another, and
‘s are independent of one-another, and 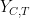 is a function of the
is a function of the 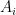 ‘s.
‘s.
Now we show that the Lipschitz Condition holds with  . Recall that the track
. Recall that the track  consists of only
consists of only 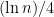 pillars. Out of the
pillars. Out of the  possible wheels
possible wheels 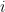 that
that 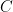 could contain, each of those wheels
could contain, each of those wheels 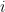 is only relevant (to the car’s stability) when the car is
is only relevant (to the car’s stability) when the car is  feet down the track for some
feet down the track for some  that places wheel
that places wheel 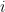 on top of a pillar. Since there are only
on top of a pillar. Since there are only  pillars, each wheel
pillars, each wheel 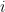 is only relevant to the train car’s stability for
is only relevant to the train car’s stability for 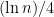 positions
positions  on the track. In other words, for a given wheel position
on the track. In other words, for a given wheel position 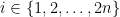 , there are only
, there are only 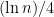 values of
values of 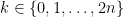 for which
for which 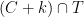 can possibly contain
can possibly contain 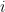 . As a result, each
. As a result, each 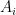 can only affect the value of
can only affect the value of 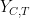 by at most
by at most 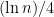 , meaning that the Lipschitz Condition holds with
, meaning that the Lipschitz Condition holds with  .
.
Applying McDiarmid’s Inequality, we can deduce that
![\displaystyle \Pr[n^{3/4} - Y_{C, T} > n^{5/8} \cdot (\ln n) / 4] \le 2e^{-n^{1/4}}.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5CPr%5Bn%5E%7B3%2F4%7D+-+Y_%7BC%2C+T%7D+%3E+n%5E%7B5%2F8%7D+%5Ccdot+%28%5Cln+n%29+%2F+4%5D+%5Cle+2e%5E%7B-n%5E%7B1%2F4%7D%7D.&bg=ffffff&fg=000000&s=0&c=20201002)
When  is large, this probability is much smaller than
is large, this probability is much smaller than  . It follows that
. It follows that
![{\Pr[X_{C, T}] = \Pr[Y_{C, T} = 0] < \frac{1}{2 \binom{4n}{(\ln n) / 4}}}](https://s0.wp.com/latex.php?latex=%7B%5CPr%5BX_%7BC%2C+T%7D%5D+%3D+%5CPr%5BY_%7BC%2C+T%7D+%3D+0%5D+%3C+%5Cfrac%7B1%7D%7B2+%5Cbinom%7B4n%7D%7B%28%5Cln+n%29+%2F+4%7D%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Summing over all possible options for the track  , the probability that any of them support the train car
, the probability that any of them support the train car 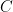 is therefore less than
is therefore less than 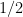 . This completes the proof: we have shown (non-constructively) that some train car
. This completes the proof: we have shown (non-constructively) that some train car 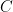 with
with  or more wheels fails to be supported by any track
or more wheels fails to be supported by any track  consisting of
consisting of  or fewer pillars.
or fewer pillars.
Conclusion. If you’ve made it to here, you might want to take a look at the paper that this blog post is based on. It turns out that there’s even more fun to be had: in fact, the train-track problem can be used to give illustrative examples of some of the most useful techniques in probabilistic combinatorics, including, e.g., the Lovász Local Lemma and the Method of Conditional Expectations!
1 This research was partially sponsored by the United States Air Force Research Laboratory and was accomplished under Cooperative Agreement Number FA8750-19-2-1000. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the United States Air Force or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein.
. It’s actually
doubles each time you increase your speed by 10 mph. Of course, what we actually care about is
, which by Bayes’ rule is
. It seems likely that both
and
increase as you drive faster, but since I only have data on how the first quantity changes, I’ll ignore changes to the second.
, but our expected time spent dead is
minutes. So our expected trip length, including time spent dead, is:
minutes.